



Complex numbers, complex numbers, complex numbers,
every where we go
pages of complex numbers applications
argand diagrams - complex number application
compex numbers, comlex numbers, cartesian form
complex
numbermagnitude and direction, use the polar form
of a complex number in engineering applications
both polar forms and rectangular forms of complex numbers
not difficult numbers, just complex numbers
complex numbers are relatively easy to learn to manipulate
addition of complex numbers in cartesian /rectangular form
conjugate and conjugation in rectangular
form and multiplication and division
complex numbers in real world applications
is not galling to those of us who also have
dra
COMPLEX NUMBERS, complex numbers, complex numbers
Argand diagrams, Cartesian form, polar form of complex numbers
The use of the complex number in engineering
Complex numbers, the Argand diagram used by Jean Louis Argand
that is the argand diagram was not invented by jean louis argand
complex numbers in cartesian form is also known as rectangular form
binomial theorem covered in next chapter
step by step instructions
for use of a calculator
make sure it is a scientific
calculator with complex number capability
real and imaginary numbers
Pythagoras theory, Pythagoras theorem
the 345 triangle or 3 4 5 triangle
an easy test of complex numbers for us to use
always use correct layout when using the conjugate
sketch of an argand diagram is always useful
individuality – an important
characteristic of fonts
complex numbers is not a state of mind, more a form of analysis
pushing cartesian or rectangular number form into polar numbers
was pythagaros a square ?
the makrobicz mathematics for cynics is for
well, cynics, like us
complex jokes are not ever funny and yet
complex numbers is no joke, as a subject
mind you, life is a bit of joke
where do all the letters go when microsoft shoves another application up on the screen
probably with all the socks that go missing from the washing machine
a complex number of warps in the fabric of the space time continuum - sock fabric probably
Argand Diagrams
Cartesian form
Polar form
Real world applications
All
those that believe in telekinesis..........raise my hand
Complex numbers are not "difficult" numbers or "complicated" numbers. Complex numbers are numbers made from more than one ordinary number. Thus, they are a "complex", a compound of more than one part.
Now that you have this in mind, let me illustrate how a complex number is formed.
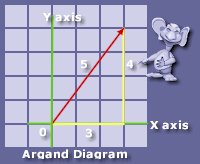
The diagram above depicts Pythagoras' famous "3,4,5" triangle, a simple right angled triangle with the sides of 3 and 4 units respectively and a hypotenuse of 5 units . You will also notice that the hypotenuse has an arrow on the upper tip. This simply depicts that the hypotenuse is a phasor (more on Phasors later). You can see that the hypotenuse has magnitude (size) as well as direction (where the arrow is pointing). Thus, the hypotenuse can be described by both of its controlling sides ( 3 and 4).
Complex numbers, in engineering in particular, are an easy way to define both magnitude and direction of a subject. Within the realms of electrical engineering, complex numbers are used to describe impedance, relative to pure resistance and reactance, whether it is the imaginary value of capacitance or inductance, especially when constructing circuits for membrane switch pads. It may be worth noting that complex numbers, are relatively simple to do the basic arithmetic processes on, providing they are kept in the appropriate form. For example, the division of complex numbers in rectangular or Cartesian form requires a somewhat lengthy process of utilising conjugates ( more on complex numbers conjugates later ). However, complex numbers can be divided quite simply using the polar form of the complex number.
When dealing with complex numbers, the numbers along the "X" axis are said to be "real" numbers. The numbers on the y axis are "imaginary" numbers. This is just a term, do not let it confuse you. With this in mind we can see a real value of 3 and an imaginary value of 4.
The way this is written depends whether it is used within an engineering environment or a purely mathematical environment. Mathematically value of the hypotenuse is 3 + 4i . Notice the i suffix for the imaginary part of the complex number. Within the realms of engineering, i is used for current so the next available letter is used, j. This would be written as 3 + j4. This format of expressing complex numbers is called "Rectangular form" or "Cartesian form"
To sum up what you have learned so far;
now for a bit of schoolboy math, remember the formula for Pythagoras' theory of right angled triangles ?
"The sum of the square of the sides is equal to the square of the hypotenuse."
let us try it out;
The sum of the square of the sides; this means we square the sides then add them together. 32 = 9 and 42 = 16. That is the sides squared, now let us add them together, 9+16 = 25.
the second part of Pythagoras' theory is that they equal the square of the hypotenuse. 25 = H2. Now all we have to do is find the value of H, which we do by finding the square root of H2 written out, it looks like this;
25 = H2
√25 = √H²
5 = H
Now the complex number can be written in Cartesian (rectangle) form as 3 + j4 = 5.
For differing or unknown values of the complex number, for instance the "H" that was used to represent the hypotenuse, a standard set of characters are used as illustrated in the diagram below;
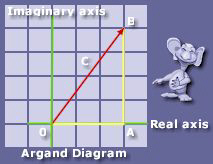
As you can readily see, this means that "c = a +jb" there are other notations used, for instance in electrical engineering, values of impedance et cetera are depicted as z for the hypotenuse. More on that later.
consider the following diagram
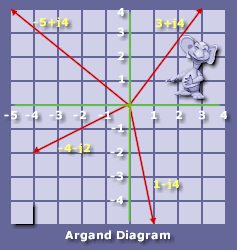
Here are plotted four phasors with their respective Cartesian complex number values. The diagram for showing these numbers is called an Argand diagram. Named after, but not invented by, Jean Robert Argand. It was, in fact, invented some years earlier by Casper Wessel.
The polar form is simply another way of expressing a complex number. We have already discussed the fact that a complex number has both magnitude and direction. We can express this by giving not only the real and imaginary values, but by giving the magnitude (length) of the hypotenuse, called the modulus, with respect to the angle between it and the real axis. The angle is referred to as the argument between the modulus and the real axis. Think about it. The irritating flash movie below illustrates the modulus and the argument.
The Polar form of a complex number is written in the following way
The C denotes the Modulus and the Greek symbol Phi represents the Argument.
That ends this introduction to complex numbers. You now know
In the next chapter we will add and subtract complex numbers in Cartesian form and polar form. Meanwhile please feel free to contact me regarding any questions or comments you may have. Please mark the heading complex numbers.
I can be reached direct via email at
Other excerpts from these articles can be viewed at
other links